大家好,我是曾续缘。今天我将为大家详细介绍在C++中构建LR(0)项集规范族和SLR(1)分析表的过程。
在编译原理中,LR(0)项集规范族和SLR(1)分析表是非常重要的概念。LR(0)项集规范族是由文法中的各个产生式的项组成的集合,它们代表了语法分析中的状态。而SLR(1)分析表则是根据LR(0)项集规范族构建的,它记录了在语法分析过程中的状态转移和动作。
在本教程中,我将逐步介绍如何在C++中实现构建LR(0)项集规范族和SLR(1)分析表的过程。我们将从定义文法的数据结构开始,然后讲解如何进行初始化操作,接着详细介绍闭包函数和状态转移函数的实现细节。通过这些讲解,您将能够清晰地理解整个过程的实现逻辑。
结构定义和预处理
定义数据结构
map<string, vector<vector<string>>>mp;
string start; // 文法开始符
set<string> nonterminal; // 非终结符
set<string>terminal; // 终结符
map<string, set<string>>first; // 每个key的first集
map<string, set<string>>follow; // 每个key的follow集
vector<string>lines; // 所有的产生式
string epsilon = "ε";工欲善其事,必先利其器,我们首先定义以上数据结构,
void init_data() {
mp.clear();
start = string::npos;
nonterminal.clear();
terminal.clear();
first.clear();
follow.clear();
lines.clear();
}每次开始前, 进行初始化操作.
按行分割产生式
我们将每行的文法产生式(如S -> b)读入为一行字符串, 将所有的产生式保存到lines中.
具体实现就是按换行符\n来分割字符串输入input.
vector<string> split_line(string input) {
vector<string> lines;
istringstream iss(input);
string line;
while (getline(iss, line, '\n')) {
lines.push_back(line);
}
return lines;
}分割带|的产生式
接着处理带有|的产生式, 这里要求输入的产生式需要使用空格来分隔每个元素, 也就是我们把每个元素视为字符串, 使用空格分隔不同字符串.
下面这个函数将类似于S -> ab | c 的产生式改为两条产生式S -> ab和S -> c.
查看代码
vector<string> solve_or(vector<string>lines) {
vector<string>ans;
for (auto line : lines) {
stringstream ss(line);
string key, arrow;
ss >> key;
ss >> arrow;
string segment;
while (getline(ss, segment, '|')) {
ans.push_back(key + " " + arrow + " " + segment);
}
}
return ans;
}引入增广文法
引入增广文法, 这里要求输入的第一个文法的左部为文法的开始符号, 并且硬编码了增广文法的开始符号为S'.
增广文法的引入有以下几个主要原因:
- 方便分析:增广文法的引入可以简化语法分析过程。通过添加一个新的开始符号和对应的产生式,可以将原文法的起始符号作为非终结符在右部出现,从而使得整个文法产生式右部不再包含原始的开始符号,简化了语法分析过程。
- 保持一致性:增广文法可以保持文法的一致性。在一些文法分析算法中,需要保证每个产生式都具有同样数量的符号,而原始文法中的开始符号只出现在左部,不出现在右部。通过引入增广文法,可以使所有产生式都符合这个要求,保持了文法的一致性。
- 唯一开始符号:增广文法确保了文法只有一个开始符号。在进行语法分析时,通常需要指定一个明确的开始符号来推导出句子的推导序列。通过引入增广文法,可以明确指定一个新的开始符号,使文法具备唯一的开始符号,方便语法分析的进行。
void extend_start() {
stringstream ss(lines[0]);
string s;
ss >> s;
lines.insert(lines.begin(), string("S' -> " + s));
start = "S'";
}文法分词
接下来这一步很重要, 之前的文法都是整条使用string来保存, 这样不好分析, 我们通过item_mp函数将字符串表示的文法识别成一个个元素, 同时对产生式左部相同的(按key值)进行分组.
查看代码
void item_mp() {
for (auto& line : lines) {
stringstream ss(line);
string key, arrow;
ss >> key;
ss >> arrow;
mp[key].push_back(vector<string>{});
while (ss >> arrow) {
mp[key].back().push_back(arrow);
}
}
}求终结符和非终结符
有了mp之后, 我们可以轻松得到非终结符、终结符.
查看代码
void get_nonterminal() {
for (auto& m : mp) {
nonterminal.insert(m.first); // 文法左部即非终结符
}
}
void get_terminal() {
for (auto& m : mp) {
for (auto& items : m.second) {
for (auto& item : items) {
if (!nonterminal.count(item)) { // 不是非终结符就是终结符
terminal.insert(item);
}
}
}
}
}求first集合
接下来是计算first集合, 终结符的first集合就只有自己本身.
求非终结符的first集合, 也就是求所有文法产生式左部的first集合.
比如说A -> BCD就是求左部A的first集合, 首先从右部的第一个B开始, first(B)的所有元素都属于是first(A)的元素, 除了空串epsilon, 因为B的空串不能代表A也能推导出空串, A能否推导出空串还受限于后面的CD. 因此, 如果B不能推导出空串, A不用受限于后面了, 直接结束, 如果B能推导出空串, 产生式相当变成了A -> CD, first(C)的所有元素也都属于是first(A)的元素, 除了空串... 以此类推. 结束时如果都能推导出空串, 则A也能推导出空串.

查看代码
void calculate_first() {
// 初始化每个非终结符的 First 集合为空
for (auto nt : nonterminal) {
first[nt] = {};
}
for (auto t : terminal) {
first[t] = { t };
}
bool updated = true;
while (updated) {
updated = false;
for (auto& m : mp) {
string nt = m.first;
for (auto& items : m.second) {
bool Continue = true;
for (auto& item : items) {
// 将其 First 集合中除 ε 外的所有元素加入 First 集合,并继续向后查找
for (auto& f : first[item]) {
if (f != epsilon && !first[nt].count(f)) {
first[nt].insert(f);
updated = true;
}
}
// 如果 item 不能推导出 ε,则停止向后查找
if (!first[item].count(epsilon)) {
Continue = false;
break;
}
}
if (Continue) {
first[nt].insert(epsilon);
}
}
}
}
}求follow集合
follow集合只针对非终结符而言的, 同时不用像求first集合那样使用文法产生式左部, 而是需要遍历文法产生式右部, 如果遍历到非终结符, 才能求这个非终结符的follow集合.
还是拿A -> BCD举例, 遍历BCD, 首先是求follow(B), 这需要遍历CD, 将first(C)除了epsilon加到follow(B)中, 如果first(C)包含空串, 接着将first(D)除了epsilon加到follow(B)中, 如果能遍历到最后, 将产生式左部A的follow(A)全都加到follow(B)中, 这样对于这条产生式求follow(B)的过程就结束了. 同理去求C和D的follow集.
注意上面的的follow(A)可能还没求出来获取不完全, 如果我们仅仅一次遍历加到follow(B)中, follow(B)可能不全, 因此我们需要额外判断是否存在某个follow集合发生变化, 如果存在变化, 我们需要重新遍历, 直到所有的follow集合不再变化为止.
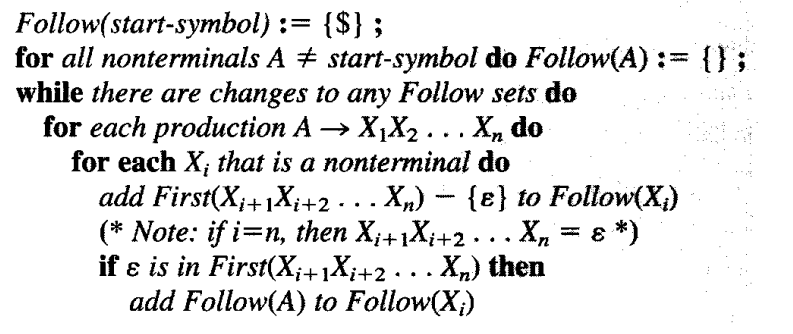
查看代码
void calculate_follow() {
// 初始化每个非终结符的 Follow 集合为空
for (auto nt : nonterminal) {
follow[nt] = {};
}
// 将开始符号的 Follow 集合初始化为 $
follow[start].insert("$");
bool updated = true;
while (updated) {
updated = false;
for (auto& m : mp) {
string nt = m.first;
for (auto& items : m.second) { // 遍历所有左部相同的产生式
for (int i = 0; i < items.size(); ++i) {
string item = items[i]; // 某条产生式右部第i个符号
if (nonterminal.count(item)) {
int j = i + 1;
// Case 1: A -> αBβ,将 First(β) - ε 加入 Follow(B)
for (; j < items.size(); ++j) {
string next_item = items[j];
if (terminal.count(next_item)) { // 这个if其实可以不写,因为first[终结符]=本身, 写出来逻辑清晰点
if(!follow[item].count(next_item)){
follow[item].insert(next_item);
updated = true;
}
break;
} else {
for (auto& f : first[next_item]) {
if (f != epsilon && !follow[item].count(f)) {
follow[item].insert(f);
updated = true;
}
}
if (!first[next_item].count(epsilon)) {
break;
}
}
}
// Case 2: A -> αB 或 A -> αBβ 且 β -> ε,将 Follow(A) 加入 Follow(B)
if (j == items.size()) {
for (auto& f : follow[nt]) {
if (!follow[item].count(f)) {
follow[item].insert(f);
updated = true;
}
}
}
}
}
}
}
}
}构建LR(0)的DFA图
定义结构
接着定义LR(0)的项集结构体和项集规范族, 和之前的mp差不多, 只是多了一个表示点的位置的整型.
查看代码
struct Item {
string left; // 产生式左部
vector<string> right; // 产生式右部
int dot_pos; // 点的位置
bool operator<(const Item& other) const {
if (left != other.left) {
return left < other.left;
}
if (right.size() != other.right.size()) {
return right.size() < other.right.size();
}
if (dot_pos != other.dot_pos) {
return dot_pos < other.dot_pos;
}
for (int i = 0; i < right.size(); ++i) {
if (right[i] != other.right[i]) {
return right[i] < other.right[i];
}
}
return false;
}
};
map<set<Item>, int> item_to_id; // 记录每个项集对应的编号
vector<set<Item>> item_sets; // 记录所有的项集
vector<vector<pair<string, int>>> transitions; // 记录状态之间的转移计算给定项集的闭包
接下来是闭包函数closure,它的作用是计算给定项集的闭包。闭包是指在项集中的每个项目后面加上可以通过产生式推导出的项目。
查看代码
// 计算闭包
set<Item> closure(const set<Item>& items, const map<string, vector<vector<string>>>& mp) {
set<Item> new_items = items;
bool updated = true;
while (updated) {
updated = false;
set<Item> temp = new_items;
for (auto& item : temp) {
if (item.dot_pos >= item.right.size()) {
continue;
}
string next_item = item.right[item.dot_pos];
if (!mp.count(next_item)) { // 如果不是非终结符,即不在任一产生式的左部,则跳过
continue; // 其实不写这个判断也行,因为使用了map,没有终结符的key,后面的for循环为空
}
for (auto& prod : mp.at(next_item)) { // 只有非终结符才会产生新的项目
Item new_item;
if (prod.size() == 1 && prod[0] == epsilon) {
new_item = { next_item, vector<string>{}, 0 }; // 产生式是S -> ε, 则项目是S -> .
} else {
new_item = { next_item, prod, 0 }; // 产生式是S -> αβ, 则项目是S -> .αβ
}
if (!new_items.count(new_item)) {
new_items.insert(new_item);
updated = true;
}
}
}
}
return new_items;
}定义状态转移函数
然后是状态转移函数goto_func,它根据给定的项集、符号和产生式映射,计算从当前项集经过给定符号进行状态转移后得到的新的项集。
查看代码
// 状态转移函数
set<Item> goto_func(const set<Item>& items, string symbol, const map<string, vector<vector<string>>>& mp) {
set<Item> new_items;
for (auto& item : items) {
if (item.dot_pos >= item.right.size()) {
continue;
}
if (item.right[item.dot_pos] == symbol) {
Item new_item = { item.left, item.right, item.dot_pos + 1 };
new_items.insert(new_item);
}
}
return closure(new_items, mp);
}构建LR(0)项集规范族
接下来是构建LR(0)项集规范族的函数construct_LR0_DFA。
查看代码
// 构建LR(0)项集规范族
void construct_LR0_DFA(const map<string, vector<vector<string>>>& mp) {
item_to_id.clear();
item_sets.clear();
transitions.clear();
set<Item> init_items;
Item start_item = { "S'", { "S" }, 0 }; // 硬编码了增广文法开始符为S', 第一个项目就是S' -> .S
init_items.insert(start_item);
init_items = closure(init_items, mp); // 对第一个项目求闭包, 得到的项集就是开始项集
item_to_id[init_items] = 0;
item_sets.push_back(init_items);
queue<set<Item>> q;
q.push(init_items);
while (!q.empty()) {
set<Item> cur_items = q.front();
q.pop();
int cur_id = item_to_id[cur_items];
for (auto& sym : nonterminal) { // 对非终结符尝试转移
set<Item> next_items = goto_func(cur_items, sym, mp);
if (!next_items.empty()) {
if (!item_to_id.count(next_items)) { // 如果是新项集, 记录下来并编号
item_to_id[next_items] = item_sets.size();
item_sets.push_back(next_items);
q.push(next_items);
}
int next_id = item_to_id[next_items];
transitions.resize(item_sets.size());
transitions[cur_id].push_back({ sym, next_id }); // 记录转移cur_id---sym--->next_id
}
}
// 和上面for循环一样, 不过需要跳过epsilon
for (auto& sym : terminal) { // 对终结符尝试转移
if (sym == epsilon)continue;
set<Item> next_items = goto_func(cur_items, sym, mp);
if (!next_items.empty()) {
if (!item_to_id.count(next_items)) {
item_to_id[next_items] = item_sets.size();
item_sets.push_back(next_items);
q.push(next_items);
}
int next_id = item_to_id[next_items];
transitions.resize(item_sets.size());
transitions[cur_id].push_back({ sym, next_id });
}
}
}
}构建SLR(1)分析表
定义结构
接下来定义SLR(1)的数据结构
map<int, map<string, string>> slr_table; // SLR(1)分析表
bool is_slr1_grammar = true; // 表示给定的文法是否满足SLR(1)语法
string confilt_msg = ""; // 用于存储冲突信息SLR(1)分析表格式为map<当前状态, map<转移字符, 得到的动作信息>>
动作信息可以是以下:
- 规约, 格式为
r数字字符串, 数字代表对应的产生式编号, 可以根据辅助函数得到具体的产生式. - 移进, 格式为
s数字字符串, 数字表示下一个状态ID. - 接受, 格式为
acc字符串, 表示接受.
定义辅助函数
当项目进行规约时, 我们需要知道是使用第几条产生式进行规约, 下面这个函数就是用来解决这个问题的.
查看代码
int find_production(const string& left, vector<string> right) {
if (right.size() == 0) {
right.push_back(epsilon);
}
for (int i = 0; i < lines.size(); ++i) {
stringstream ss(lines[i]);
string key, arrow;
ss >> key;
ss >> arrow;
if (key == left) {
vector<string> prod;
string s;
while (ss >> s) {
prod.push_back(s);
}
if (prod == right) {
return i;
}
}
}
return -1;
}该函数的作用是判断给定的一组项目中是否包含接受项目(S' -> S.)。
bool contains_accept_item(const set<Item>& items) {
for (auto& item : items) {
if (item.dot_pos == item.right.size() && item.left == start) {
return true;
}
}
return false;
}判断归约-归约冲突
规约是指将一个产生式右部的符号串替换为产生式左部的非终结符号的操作。在一个项集中, 如果有两个及以上的项目同时进行规约, 并且它们的下一个可能读取字符(即follow字符)有相同的情况, 就会产生规约规约冲突.
比如说S -> a.和B -> b.都可以规约了, 规约后为S和B, 此时S可以读取的字符有g, B可以读取的字符也有g, 如果下一个字符读取的恰巧是g, 只能规约一个那就不知道规约S好还是B好了.
查看代码
// 判断是否存在归约-归约冲突
bool hasReduceReduceConflict(const set<Item>& items) {
vector<string> reduce_symbols; // 归约符号
for (auto& item : items) {
if (item.dot_pos >= item.right.size()) { // .在最后, 为归约项目
string reduce_symbol = item.left;
if (find(reduce_symbols.begin(), reduce_symbols.end(), reduce_symbol) == reduce_symbols.end()) {
reduce_symbols.push_back(reduce_symbol); // 记录项目的左部为归约符号
}
}
}
// 检查归约-归约冲突
int num_reduce_symbols = reduce_symbols.size();
for (int i = 0; i < num_reduce_symbols; ++i) {
for (int j = i + 1; j < num_reduce_symbols; ++j) {
string reduce_symbol_1 = reduce_symbols[i];
string reduce_symbol_2 = reduce_symbols[j];
set<string> follow_1 = follow[reduce_symbol_1];
set<string> follow_2 = follow[reduce_symbol_2];
set<string> intersection;
set_intersection(follow_1.begin(), follow_1.end(),
follow_2.begin(), follow_2.end(),
inserter(intersection, intersection.begin()));
// 任意两个规约符号的follow集两两相交, 如果非空, 则出现归约-归约冲突, 记录在confilt_msg中
if (intersection.empty())continue;
is_slr1_grammar = false;
int state_id = item_to_id[items];
confilt_msg += "归约-归约冲突: 状态" + to_string(state_id) +
"中规约项存在Follow(" + reduce_symbol_1 + ")∩Follow(" + reduce_symbol_2 + ") = ";
for (auto s : intersection) {
confilt_msg += s + ",";
} confilt_msg.back() = '\n';
}
}
return is_slr1_grammar;
}判断移进-归约冲突
移进规约冲突就是移进符号在规约符号的follow集中
查看代码
bool hasShiftReduceConflict(const set<Item>& items) {
vector<Item>reduce_item;
for (auto& item : items) {
if (item.dot_pos == item.right.size()) {
reduce_item.push_back(item);
}
}
for (auto& item : items) {
if (item.dot_pos == item.right.size())continue;
if (nonterminal.count(item.right[item.dot_pos]))continue;
string shift_symbol = item.right[item.dot_pos];
for (auto it : reduce_item) {
if (follow[it.left].count(shift_symbol)) {
is_slr1_grammar = false;
int state_id = item_to_id[items];
confilt_msg += "移进-归约冲突: 状态" + to_string(state_id) +
"中移进终结符" + shift_symbol + "存在于规约follow(" + it.left + ")中\n";
}
}
}
return is_slr1_grammar;
}判断slr1文法
判断是否是slr1文法, 也就是看是否存在归约-归约冲突或移进-归约冲突.
查看代码
void check_slr1() {
is_slr1_grammar = true;
confilt_msg = "";
for (auto items : item_sets) {
hasReduceReduceConflict(items);
}
for (auto items : item_sets) {
hasShiftReduceConflict(items);
}
}构建slr1状态转移表
查看代码
void construct_SLR1_table() {
// 清空SLR(1)分析表
slr_table.clear();
if (!is_slr1_grammar)return;
// 构建状态转移表
for (int i = 0; i < item_sets.size(); ++i) {
for (auto& transition : transitions[i]) {
string symbol = transition.first;
int next_state_id = transition.second;
if (terminal.count(symbol)) {
// 终结符则是移进操作
slr_table[i][symbol] = "s" + to_string(next_state_id);
} else {
// 非终结符则是转移操作
slr_table[i][symbol] = to_string(next_state_id);
}
}
}
// 构建规约表
for (int i = 0; i < item_sets.size(); ++i) {
for (auto& item : item_sets[i]) {
if (item.dot_pos == item.right.size()) {
// 规约项目
if (item.left == start) {
// 对于接受项目,采用acc表示接受
slr_table[i]["$"] = "acc";
} else {
// 查找对应的产生式编号
int production_id = find_production(item.left, item.right);
if (production_id != -1) {
// 对于对应的终结符,采用r加产生式编号表示规约
for (auto& term : follow[item.left]) {
if (slr_table[i].count(term))continue;
slr_table[i][term] = "r" + to_string(production_id);
}
}
}
}
}
}
}构建完成后, slr1的状态转移表的所有信息都保存到了map<int, map<string, string>> slr_table中. 格式为map<当前状态, map<转移字符, 得到的动作信息>>
展示分析过程
有了slr1分析表slr_table后, 我们就可以分析一个具体的句子了, 前提是这个句子符合分析表对应的文法规则.
定义结构
查看代码
vector<string> input;
vector<string> parse_stack;
string action = "";
vector<vector<string>>line;
vector<vector<vector<string>>>table;
int state = 0;
class ConcreteSyntaxTreeNode {
public:
string value; // 节点值,可以是终结符或非终结符
vector<ConcreteSyntaxTreeNode*> children; // 子节点
ConcreteSyntaxTreeNode(string val) : value(val) {}
~ConcreteSyntaxTreeNode() {
for (auto child : children) {
delete child;
}
}
};
vector<ConcreteSyntaxTreeNode*> SyntaxTree;input存储输入句子, parse_stack存储分析栈的内容, action存储某一次的动作内容,
line存储每一个步骤的parse_stack,input, action,
table存储所有的line.
ConcreteSyntaxTreeNode结构体表示分析树的节点,
特别要注意的是,后续操作需要支持删除第一个元素的功能。在这里选择了vector数据结构而不是deque,是为了更容易理解,而不是因为我技术水平无法实现。
SyntaxTree表示分析过程中产生的分析树的节点, 如果分析成功, 最终会存下一个分析树的根节点.
输入句子
我们使用vector<string> input来存储经过分词后的输入句子, 每个string代码句子中的一个词.
分词的方法可以是使用正则表达式进行匹配后得到,
也可以是约束输入方式, 用简单的分词函数进行, 比如规定每个词之间存在一个空格, 之后按空格分词.
初始化
初始状态为state = 0,
将结束符号"$"添加到输入字符串的末尾
input.push_back("$");将初始状态"0"和结束符号"$"压入分析栈。
parse_stack.push_back("$");
parse_stack.push_back("0");分析过程
构建分析树的过程和语法分析的过程同时进行,
直到acc为止, 不断执行以下操作:
首先获取分析栈的顶部状态作为当前状态
state根据当前状态和输入字符串的下一个符号可以得到SLR(1)分析表的下一个动作
动作可以是移进(s)、规约(r)或接受(acc), 根据动作执行相应的操作:
移进(
s数字):将输入字符串的下一个符号移进分析栈,并将该符号对应的节点添加到语法树中。然后,从输入字符串中删除该符号。规约(
r数字):根据规约产生式,从分析栈中弹出相应的符号, 其中的状态也一并弹出,并将这些符号对应的节点组合成一个新的节点,添加到语法树中。然后,将规约产生式的左部符号移进分析栈。接受(
acc):分析成功,执行完这次循环体后退出循环。
将当前的分析栈、输入字符串和执行的动作存储到分析表中。
查看代码
while (!ok) {
state = fint(parse_stack.back());
vector<vector<string>>line;
line.push_back(parse_stack);
line.push_back(input);
string action = "";
string cur = *input.begin();
string action_entry = slr_table[state][cur];
if (action_entry[0] == 'r') {
string line = barparent->reduce_production(action_entry);
action = "用" + line + "规约";
stringstream ss(line);
string key, arrow;
ss >> key;
ss >> arrow;
vector<string>item;
ConcreteSyntaxTreeNode* root = new ConcreteSyntaxTreeNode(key);
while (ss >> arrow) {
item.push_back(arrow);
}
while (item.size() && item.back() != epsilon) {
while (parse_stack.back() != item.back()) {
parse_stack.pop_back(); // pop 状态
}
root->children.insert(root->children.begin(), SyntaxTree.back());
SyntaxTree.pop_back();
parse_stack.pop_back(); // pop 符号
item.pop_back();
}
SyntaxTree.push_back(root);
state = fint(parse_stack.back()); //栈状态
parse_stack.push_back(key); // 规约字符
parse_stack.push_back(slr_table[state][key]);
} else if (action_entry[0] == 's') {
action = "移进" + action_entry.substr(1);
ConcreteSyntaxTreeNode* root = new ConcreteSyntaxTreeNode(cur);
SyntaxTree.push_back(root);
parse_stack.push_back(cur); // push 符号
parse_stack.push_back(action_entry.substr(1)); // push 状态
input.erase(input.begin());
} else if (action_entry == "acc") {
action = "接受";
ok = 1;
}
line.push_back(vector<string>{action});
table.push_back(line);
}通过不断查询SLR(1)分析表和执行相应的动作,最终可以将输入字符串转换成一棵具体的语法树,也就是分析树,同时完成对输入字符串的语法分析。
特定语言抽象语法树
上面实现的分析树, 也称为具体语法树(Concrete Syntax Tree, CST), 在语法分析层面保留了源代码中的所有细节,包括括号、语法符号等, 但在语义分析上就显得庞大和臃肿了,
接下来我们构建抽象语法树(Abstract Syntax Tree, AST), 这是对源代码结构的抽象表示,它去掉了分析树中的一些不影响程序语义的细节, 只包含源代码中与程序语义相关的部分,如表达式、声明、控制流语句等。
这里的做法是对每个产生式定义语义动作, 在语法分析时根据语义动作修改具体语法树, 进而得到更简便的语法树, 即为抽象语法树.
选定特定语言
因为需要根据具体的产生式定义具体的动作, 所以我们需要为特定语言书写特定的语义动作代码. 这里我们选用TINY语言为例.
下面是TINY语言的所有文法
查看代码
program -> stmt-sequence
stmt-sequence -> stmt-sequence ; statement | statement
statement -> if-stmt | repeat-stmt | assign-stmt | read-stmt | write-stmt
if-stmt -> if exp then stmt-sequence end | if exp then stmt-sequence else stmt-sequence end
repeat-stmt -> repeat stmt-sequence until exp
assign-stmt -> identifier := exp
read-stmt -> read identifier
write-stmt -> write exp
exp -> simple-exp comparison-op simple-exp | simple-exp
comparison-op -> < | = | <= | <> | >= | >
simple-exp -> simple-exp addop term | term
addop -> + | -
term -> term mulop factor | factor
mulop -> * | / | %
factor -> ( exp ) | number | identifier根据之前的程序,对上述文法生成的产生式如下
查看代码
(0) S' -> program
(1) program -> stmt-sequence
(2) stmt-sequence -> stmt-sequence ; statement
(3) stmt-sequence -> statement
(4) statement -> if-stmt
(5) statement -> repeat-stmt
(6) statement -> assign-stmt
(7) statement -> read-stmt
(8) statement -> write-stmt
(9) if-stmt -> if exp then stmt-sequence end
(10) if-stmt -> if exp then stmt-sequence else stmt-sequence end
(11) repeat-stmt -> repeat stmt-sequence until exp
(12) assign-stmt -> identifier := exp
(13) read-stmt -> read identifier
(14) write-stmt -> write exp
(15) exp -> simple-exp comparison-op simple-exp
(16) exp -> simple-exp
(17) comparison-op -> <
(18) comparison-op -> =
(19) comparison-op -> <=
(20) comparison-op -> <>
(21) comparison-op -> >=
(22) comparison-op -> >
(23) simple-exp -> simple-exp addop term
(24) simple-exp -> term
(25) addop -> +
(26) addop -> -
(27) term -> term mulop factor
(28) term -> factor
(29) mulop -> *
(30) mulop -> /
(31) mulop -> %
(32) factor -> ( exp )
(33) factor -> number
(34) factor -> identifier定义结构
查看代码
class TINY_Node {
public:
string type;
string value;
vector<TINY_Node*>children;
TINY_Node* sibling;
TINY_Node(){
sibling = nullptr;
}
};
vector<TINY_Node*> Node_stack;TINY_Node结构体为抽象语法树的结点, 其中type是结点类型, 如果是值的结点, 值存储到value中, children是它的子节点, sibling是它的兄弟结点.
- 子节点:每个节点可以有多个子节点,代表语法结构的组成部分。例如,
if语句的节点会有子节点代表条件表达式和语句块。 - 兄弟节点:在AST中,兄弟节点表示并列的结构,如多个语句或表达式。在
TINY语言中,由分号分隔的语句会形成兄弟关系。
Node_stack类似于之前的SyntaxTree, 存储分析过程中的结点, , 如果分析成功, 最终会存下一个抽象语法树的根结点.
定义语义动作
根据规约的产生式编号编写对应的语义动作.
查看代码
void do_TINY_action(string reduce_num) {
reduce_num = reduce_num.substr(1);
//(2) stmt-sequence -> stmt-sequence ; statement
if (reduce_num == "2") {
TINY_Node* statement = Node_stack.back();Node_stack.pop_back();
TINY_Node* stmt_sequence = Node_stack.back();Node_stack.pop_back();
if (stmt_sequence->sibling == nullptr) {
stmt_sequence->sibling = statement;
} else {
stmt_sequence->sibling->sibling = statement;
}
Node_stack.push_back(stmt_sequence);
}
//(9) if-stmt -> if exp then stmt-sequence end
if (reduce_num == "9") {
TINY_Node* stmt_sequence = Node_stack.back();Node_stack.pop_back();
TINY_Node* exp = Node_stack.back();Node_stack.pop_back();
TINY_Node* if_node = Node_stack.back();Node_stack.pop_back();
if_node->children.push_back(exp);
if_node->children.push_back(stmt_sequence);
Node_stack.push_back(if_node);
}
//(10) if-stmt -> if exp then stmt-sequence else stmt-sequence end
if (reduce_num == "10") {
TINY_Node* stmt_sequence_else = Node_stack.back();Node_stack.pop_back();
TINY_Node* stmt_sequence_if = Node_stack.back();Node_stack.pop_back();
TINY_Node* exp = Node_stack.back();Node_stack.pop_back();
TINY_Node* if_node = Node_stack.back();Node_stack.pop_back();
if_node->children.push_back(exp);
if_node->children.push_back(stmt_sequence_if);
if_node->children.push_back(stmt_sequence_else);
Node_stack.push_back(if_node);
}
//(11) repeat-stmt -> repeat stmt-sequence until exp
if (reduce_num == "11") {
TINY_Node* exp = Node_stack.back();Node_stack.pop_back();
TINY_Node* stmt_sequence = Node_stack.back();Node_stack.pop_back();
TINY_Node* repeat = Node_stack.back();Node_stack.pop_back();
TINY_Node* node = repeat;
node->children.push_back(stmt_sequence);
node->children.push_back(exp);
Node_stack.push_back(node);
}
//
//(12) assign-stmt -> identifier := exp
if (reduce_num == "12") {
TINY_Node* exp = Node_stack.back();Node_stack.pop_back();
TINY_Node* assign = Node_stack.back();Node_stack.pop_back();
TINY_Node* identifier = Node_stack.back();Node_stack.pop_back();
TINY_Node* node = assign;
node->children.push_back(identifier);
node->children.push_back(exp);
Node_stack.push_back(node);
}
//
//(13) read-stmt -> read identifier
if (reduce_num == "13") {
TINY_Node* identifier = Node_stack.back();Node_stack.pop_back();
TINY_Node* read = Node_stack.back();Node_stack.pop_back();
TINY_Node* node = read;
node->children.push_back(identifier);
Node_stack.push_back(node);
}
//
//(14) write-stmt -> write exp
if (reduce_num == "14") {
TINY_Node* exp = Node_stack.back();Node_stack.pop_back();
TINY_Node* write = Node_stack.back();Node_stack.pop_back();
TINY_Node* node = write;
node->children.push_back(exp);
Node_stack.push_back(node);
}
//
//(15) exp -> simple-exp comparison-op simple-exp
if (reduce_num == "15") {
TINY_Node* simple_exp2 = Node_stack.back();Node_stack.pop_back();
TINY_Node* comparison_op = Node_stack.back();Node_stack.pop_back();
TINY_Node* simple_exp1 = Node_stack.back();Node_stack.pop_back();
TINY_Node* node = comparison_op;
node->children.push_back(simple_exp1);
node->children.push_back(simple_exp2);
Node_stack.push_back(node);
}
//(23) simple-exp -> simple-exp addop term
if (reduce_num == "23") {
TINY_Node* term = Node_stack.back();Node_stack.pop_back();
TINY_Node* addop = Node_stack.back();Node_stack.pop_back();
TINY_Node* simple_exp = Node_stack.back();Node_stack.pop_back();
TINY_Node* node = addop;
node->children.push_back(simple_exp);
node->children.push_back(term);
Node_stack.push_back(node);
}
//(27) term -> term mulop factor
if (reduce_num == "27") {
TINY_Node* factor = Node_stack.back();Node_stack.pop_back();
TINY_Node* mulop = Node_stack.back();Node_stack.pop_back();
TINY_Node* term = Node_stack.back();Node_stack.pop_back();
TINY_Node* node = mulop;
node->children.push_back(term);
node->children.push_back(factor);
Node_stack.push_back(node);
}
}在分析中生成结点
辅助函数
对于特定的token, 在移进时生成对应的结点.
有一些token, 只作为规约的标志, 没有不需要生成结点.
bool ignore_tiny_token(string s) {
if (s == "then")return true;
if (s == "else")return true;
if (s == "end")return true;
if (s == "until")return true;
if (s == "semicolon")return true;
return false;
}ignore_tiny_token返回true的token, 不需要为其生成结点.
AST的构建过程
- 移进操作:
- 在移进操作中,分析器会为每个输入的
token生成一个节点。然而,对于AST来说,只有那些对程序语义有影响的token才会生成节点,一些辅助性的token(如分隔符)则会被忽略。
- 在移进操作中,分析器会为每个输入的
- 规约操作:
- 当分析器根据语法规则进行规约时,它会从栈中弹出与规则右部相对应的节点,并执行语义动作。这些动作决定了如何将这些节点组合成新的AST节点。
- 与分析树不同,AST在规约时通常不会为每个规则创建新的根节点。相反,它会选择一个现有的、对语义重要的节点作为新结构的根,并将其他节点作为其子节点或兄弟节点。
- 语义动作:
- 语义动作是在规约时触发的,它们负责创建和修改AST节点。例如,对于
if语句,语义动作会创建一个if节点,并将条件表达式和语句序列作为其子节点。 - 语义动作还负责处理节点之间的兄弟关系,例如在语句序列中,分号分隔的多个语句会以兄弟节点的形式连接起来。
- 语义动作是在规约时触发的,它们负责创建和修改AST节点。例如,对于
构建过程再总结
构建抽象语法树的过程和语法分析的过程同时进行,
而构建抽象语法树的过程和构建分析树的过程类似, 只是在分析过程中不断简化分析树,不同之处在于:
在移进时
- 分析树为每个输入
token生成结点 - 而语法树只为重要的
token生成结点
- 分析树为每个输入
在规约时
- 分析树首先生成一个根结点, 然后将产生式右部相关的结点作为根结点的子结点
- 语法树不生成新的结点, 而是从产生式右部相关的结点中选择重要的结点作为根结点, 其余结点作为兄弟结点或子结点
重要的结点指的是操作符结点或者那些语法控制字符, 比如+, if等.
兄弟结点体现在语句序列, 在TINY语言中是以分号作为标志的,
子结点就是每种操作的子结构, 比如说if结点有判断部分子结点, 判断为真部分, 可选的判断为假部分, 共2或3个子结点.
特定语言中间代码
中间代码是在编译过程中生成的一种介于高级语言和机器语言之间的代码,它简化了源代码的结构,便于后续的代码优化和目标代码生成。
我们选定的中间代码格式为P-代码,为了简便,我们的P-代码程序只包含代码存储器、临时数据栈。
定义结构
code_line:这是一个字符串向量,用于存储P-代码的指令行,相当于代码存储器。lable_stack:这是一个字符串向量,用于管理跳转标签,用于条件跳转和循环结构。label:这是一个整型变量,用于生成唯一的标签。
为了方便展示,将跳转标签栈从临时数据栈中抽离出来,使用lable_stack表示跳转标签栈,临时数据栈使用递归实现。
查看代码
vector<string>code_line;
vector<string>lable_stack;
int label = 0;
string newLabel() {
lable_stack.push_back("L" + to_string(++label));
return lable_stack.back();
}
string curLabel() {
return lable_stack.back();
}
string useLable() {
string ans = lable_stack.back();
lable_stack.pop_back();
return ans;
}中间代码生成
其实抽象语法树也是一种中间表示形式,可以说是图形化的表示,
而P-代码也是一种中间表示形式,可以从抽象语法树中得到。
具体来说,实现一个函数tiny_generateIntermediateCode,接受一个代表抽象语法树的节点,然后递归地遍历这个树,生成对应的中间代码。
中间代码生成是编译过程中的一个关键阶段,它将抽象语法树(AST)转换为一组中间表示形式的代码,通常是介于高级语言和机器语言之间的一种代码。在这个例子中,我们使用P-代码作为中间表示形式。下面是中间代码生成的详细过程:
初始化
- 创建一个空白的代码行向量
code_line,用于存储生成的P-代码指令。 - 创建一个标签栈
lable_stack,用于管理跳转标签。 - 初始化标签计数器
label,用于生成唯一的标签。
递归遍历AST
- 从AST的根节点开始,递归地遍历整个树。
- 对于每个节点,根据其类型生成相应的P-代码指令。
生成P-代码指令
- 输入/输出操作(read/write):
- 首先生成操作数的代码(即读取或写入的变量)。
- 然后向
code_line中添加一条读取或写入栈顶元素的指令。
- 条件语句(if):
- 首先生成条件表达式的代码。
- 生成一个新标签,并添加一条跳转指令(fjp),如果条件为假,则跳转到该标签。
- 然后生成if语句块中的代码。
- 如果存在else部分,生成else部分的代码。
- 最后,从标签栈中移除当前标签。
- 赋值语句(assign):
- 首先生成左右操作数的代码。
- 然后添加一条赋值指令,将栈顶的第二个元素赋值给第一个元素。
- 算术和比较操作(mulop/addop/comparison-op):
- 首先生成操作数的代码。
- 然后添加一条计算或比较指令,根据操作符执行相应的操作。
- 循环语句(repeat):
- 生成一个新标签,并添加一条标签指令,标记循环的开始。
- 然后生成循环体的代码。
- 生成循环条件代码,并添加一条条件跳转指令,如果条件为假,则跳回到循环开始的地方。
- 最后,从标签栈中移除当前标签。
- 标识符和数字(identifier/number):
- 直接添加一条将它们压入栈中的指令。
处理兄弟节点
- 在处理完当前节点后,递归调用处理兄弟节点,实现整个AST的遍历。
完成中间代码生成
- 当所有节点都被处理完毕后,
code_line中将包含完整的P-代码指令集。 - 这组指令可以被后续的编译阶段使用,例如代码优化或目标代码生成。
通过这个过程,编译器将高级语言的抽象语法树转换为一组中间代码指令,这些指令既保留了源代码的语义,又简化了其结构,便于后续的处理。
查看代码
void tiny_generateIntermediateCode(TINY_Node* node) {
if (node == nullptr)return ;
if (node->type == "read" ||
node->type == "write") {
tiny_generateIntermediateCode(*node->children.begin());
code_line.push_back(node->type + "\t; 读取栈顶元素,执行操作");
} else if (node->type == "if") {
tiny_generateIntermediateCode(node->children[0]);
newLabel();
code_line.push_back("fjp " + curLabel() + "\t; 读取栈顶布尔值,如果为假,跳转至标签" + curLabel() + "处");
tiny_generateIntermediateCode(node->children[1]);
code_line.push_back("label " + lable_stack.back() + "\t; 标签" + curLabel() + "定义处");
if (node->children.size() == 3) {
tiny_generateIntermediateCode(node->children[2]);
}
useLable();
} else if (node->type == "assign") {
tiny_generateIntermediateCode(node->children[0]);
tiny_generateIntermediateCode(node->children[1]);
code_line.push_back("assign \t; 读取栈顶第一个元素,赋值为读取栈顶第二个元素的值");
} else if (
node->type == "mulop" ||
node->type == "addop"
) {
tiny_generateIntermediateCode(node->children[0]);
tiny_generateIntermediateCode(node->children[1]);
code_line.push_back("calc " + node->value + "\t; 读取栈顶元素作为算符右值,第二个为左值,执行算符计算,将算术值压入栈中");
} else if (
node->type == "comparison-op"
) {
tiny_generateIntermediateCode(node->children[0]);
tiny_generateIntermediateCode(node->children[1]);
code_line.push_back("comp " + node->value + "\t; 读取栈顶元素作为算符右值,第二个为左值,执行算符比较,将结果布尔值压入栈中");
} else if (node->type == "repeat") {
newLabel();
code_line.push_back("label " + lable_stack.back() + "\t; 标签" + lable_stack.back() + "定义处");
tiny_generateIntermediateCode(node->children[0]);
tiny_generateIntermediateCode(node->children[1]);
code_line.push_back("fjp " + curLabel() + "\t; 读取栈顶布尔值,如果为假,跳转至标签" + curLabel() + "处");
useLable();
} else if (node->type == "identifier" || node->type == "number") {
code_line.push_back("load " + node->value + "\t; 将值" + node->value + "压入栈中");
}
tiny_generateIntermediateCode(node->sibling);
}以上就是分享的全部内容,希望本教程能对您有所帮助,为您在编写自己的语法分析器时提供有益的参考。
如果大家有任何问题或疑惑,都可以随时向我提问。我会尽力帮助大家解决。
如果需要完整的有图形界面展示的代码,请在下方留言哦。
