大家好，我是曾续缘。今天为大家讲解编译原理中一个非常重要的主题：如何利用正则表达式来绘制NFA图，并将其转换为DFA。我们还将学习如何对DFA进行最小化，并最终生成相应的C++代码。有了c++源代码后，我们对其编译得到可执行程序，就可以利用这个可执行程序来进行词法分析了。

正则表达式→后缀表示

正则表达式就好比中缀算术表达式, 都需要考虑运算符的优先级和括号的匹配等复杂问题, 计算机不好处理. 将中缀算术表达式转为后缀后就可以明确地指定运算符的位置和计算顺序，从而减少对优先级和括号匹配的依赖。同理, 我们使用类似的方法将正则表达式转换为后缀的形式.

定义常量

首先需要选一些不常用的字符作为常量。

const char connector = '`';
const char epsilon = '$';

定义优先级比较函数

接着定义两个函数（isp和icp）用于中缀表达式转换为后缀表达式时使用的栈中正则运算符优先级比较函数。

isp函数（In-Stack Priority）用于确定运算符在栈内的优先级。

icp函数（In-Coming Priority）用于确定运算符在栈外的优先级。

为什么要区分栈内和栈外的运算符优先级？ 这是因为某一操作符按照算正则运算有一个优先级，这是icp。一旦它进入操作符栈，它的优先级要提高，以体现优先级相同的操作符先来的先做，就是说，在表达式中运算优先级相同的必须自左向右运算，这就是栈内优先级isp。

查看代码

// isp
int isp(char c) {
    switch (c) {
        case epsilon: return 0;
        case '(': return 1;
        case '*': case '?': case '+': return 7;
        case '|': return 5;
        case connector: return 3;
        case ')': return 8;
        default: break;
    }
    cerr << "isp error\n";
    return -1;
}

// icp
int icp(char c) {
    switch (c) {
        case epsilon: return 0;
        case '(': return 8;
        case '*': case '?': case '+': return 6;
        case '|': return 4;
        case connector: return 2;
        case ')': return 1;
    }
    cerr << "icp error!\n";
    return -1;
}

运算符的优先级如下所示（从高到低）：

1. '(' 和 ')': 括号具有最高的优先级，用于控制运算符的结合性。
2. '*'、'?'、'+': 这些是正则表达式中的重复操作符，具有较高的优先级。
3. '|': 表示或操作，其优先级在 '+'、'?'、'*' 之下，但高于连接操作。
4. 连接操作符：表示连接，具有最低的优先级。

优先级较高的运算符会先入栈，较低的优先级则后入栈。

区分运算符和非运算符

// 区分运算符和非运算符
bool is_not_regex_op(char c) {
    switch (c) {
        case epsilon: case '(': case '*': case '?': case '+': case '|': case connector: case ')': return false;
    }
    return true;
}

字符串预处理

转义字符预处理

对正则表达式进行预处理包括两个主要步骤：

1. 处理转义字符：对于正则表达式中的转义字符，如'\'+'n'、'\'+'t'，需要将其真正转换为对应的转义字符。例如，'\'+'n'转换为换行符\n，'\'+'t'转换为制表符\t。
2. 处理与正则表达式符号冲突的字符：在正则表达式中，有些字符具有特殊含义，如+、*等，如果需要匹配它们本身，需要进行转义。因此，如果输入的正则表达式中包含与这些特殊字符冲突的字符，需要将其转换为其他不常用的字符，以避免与正则表达式的语法产生冲突。例如，将输入的'\'+'+'转换为(char)-128，将'\'+'*'转换为(char)-127。

查看代码

// 对正则表达式预处理
// 1. 对于正则表达式中的转义字符，需要真正的转为转义字符，如'\'+'n'转为'\n'
// 2. 对于语法中与正则表达式符号冲突的字符，输入是经过转义字符的，处理上是将其转为其他不常用的字符，如'\'+'*'转为(char)-127
string preprocessing(string regex) {
	string ans = "";
	for (int i = 0; i < regex.size(); i++) {
		if (regex[i] == '\\') {
			if (i + 1 < regex.size()) {
				if (regex[i + 1] == 'n') {
					ans += '\n';
				} else if (regex[i + 1] == 't') {
					ans += '\t';
				} else if (regex[i + 1] == '+') {
					ans += (char)-128;
				} else if (regex[i + 1] == '*') {
					ans += (char)-127;
				}
				else {
					return "";
				}
				i++;
			} else {
				return "";
			}
		} else {
			ans += regex[i];
		}
	}
	return ans;
}

添加连接符

因为在正则表达式中, 字符相连也算是一种运算, 比如说ab, 就是匹配a再匹配b,是一种运算, 因此需要在ab之间加一个运算符(也就是之前定义的元符号connector). 当然除了字符相连这种情况, 还有 ( 的情况

查看代码

string add_connector(string regex) {
	string ans = "";
	char cur = regex[0], pre = connector;
	for (int i = 1; i < regex.size(); i++) {
		pre = regex[i - 1];
		cur = regex[i];
		ans += pre;
		if (pre != '(' && pre != '|' && (is_not_regex_op(cur) || cur == '(')) {
			ans += connector;
		}
	}
	ans += cur;
	return ans;
}

转后缀表示

查看代码

string to_postfix(string regex) {
	string ans = "";
	regex += epsilon;
	stack<char>s;
	s.push(epsilon);
	auto cur = regex.begin();
	char op;
	while (!s.empty()) {
		if (is_not_regex_op(*cur)) {
			ans += *cur++;
		} else {
			op = s.top();
			if (isp(op) < icp(*cur)) {
				s.push(*cur++);
			} else if (isp(op) > icp(*cur)) {
				ans += op;
				s.pop();
			} else {
				s.pop();
				if (op == '(') {
					cur++;
				}
			}
		}
	}
	return ans;
}

后缀正则表达式→NFA

有了后缀表示的正则表达式，就可以很方便的得到对应的NFA了。

首先定义状态, 从0开始计数, 每次新建状态使用new_state函数来创建.

int state = 0;
int new_state() {
	return state++;
}
void init_state() { 
	state = 0; 
}

接下来定义正则表达式的图结构体. 类似于下图

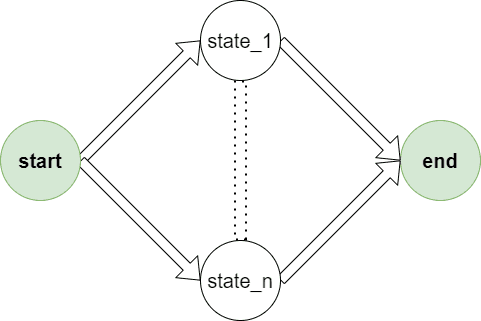
图的两要素有点和边. 点就是上面定义的状态, 边是下面定义的edge, 有起始状态u、转移字符w、结束状态v.

边里边记录了点, 那么完整的正则表达式图结构体就是所有边的集合了, 当然我们还需要区分整个正则表达式的起始和结束状态, 使用两个整型start和end来记录.

每个新建的图开始时没有边的转移关系, 使用两个状态表示起始和结束状态即可, 类似于下图

查看代码

struct edge {
	int u;
	int v;
	char w;
	edge() = default;
	edge(int _u, int _v, char _val) : w(_val) {
		u = _u;
		v = _v;
	}
	edge(char _val) : w(_val) {
		u = new_state();
		v = new_state();
	}
};


struct CompareEdge {
	bool operator()(const edge& e1, const edge& e2) const {
		if (e1.u != e2.u) {
			return e1.u < e2.u;
		} else if (e1.v != e2.v) {
			return e1.v < e2.v;
		} else {
			return e1.w < e2.w;
		}
	}
};
struct graph {
	set<edge, CompareEdge>edges;
	int start;
	int end;
	graph() = default;
	graph(int _start, int _end) {
		start = _start;
		end = _end;
	};
	graph(edge e) {
		edges.insert(e);
		start = e.u;
		end = e.v;
	}
};
graph new_graph() {
	int start = new_state();
	int end = new_state();
	return graph(start, end);
}

接下来是正则表达式转换为NFA的函数。它接受一个后缀表示的正则表达式作为输入，并返回一个表示该正则表达式对应的NFA的图。

我们使用栈作为辅助，遍历输入的正则表达式的每个字符，根据字符的类型执行相应的操作：

• 如果字符是竖线（|），则从栈中弹出两个图，将它们合并为一个新的图，并将新图压入栈中。
• 如果字符是星号（*），则从栈中弹出一个图，对该图进行闭包操作，并将结果图压入栈中。
• 如果字符是加号（+），则从栈中弹出一个图，对该图进行正闭包操作，并将结果图压入栈中。
• 如果字符是问号（?），则从栈中弹出一个图，对该图进行可选操作，并将结果图压入栈中。
• 如果字符是连接符（connector），则从栈中弹出两个图，将它们连接为一个新的图，并将新图压入栈中。
• 否则就是新状态的情况，将字符转换为一个边的图，并将该图压入栈中。

最后，从栈中弹出最后一个图，即为转换后的NFA，然后将其返回。

查看代码

graph regex_to_nfa(string regex) {
	graph nfa, tmp, l, r;
	stack<graph>s;
	char ch;
	for (int i = 0; i < regex.size(); i++) {
		ch = regex[i];
		switch (ch) {
		case '|':
			r = s.top();s.pop();
			l = s.top();s.pop();
			tmp = unite(l, r);
			s.push(tmp);
			break;
		case '*':
			l = s.top();s.pop();
			tmp = closure(l);
			s.push(tmp);
			break;
		case '+':
			l = s.top();s.pop();
			tmp = positive_closure(l);
			s.push(tmp);
			break;
		case '?':
			l = s.top();s.pop();
			tmp = optional(l);
			s.push(tmp);
			break;
		case connector:
			r = s.top();s.pop();
			l = s.top();s.pop();
			tmp = concat(l, r);
			s.push(tmp);
			break;
		default:
			if (ch == (char)-128) {
				ch = '+';
			} else if (ch == (char)-127) {
				ch = '*';
			}
			tmp = graph(edge(ch));
			s.push(tmp);
			break;
		}
	}
	nfa = s.top();s.pop();
	return nfa;
}

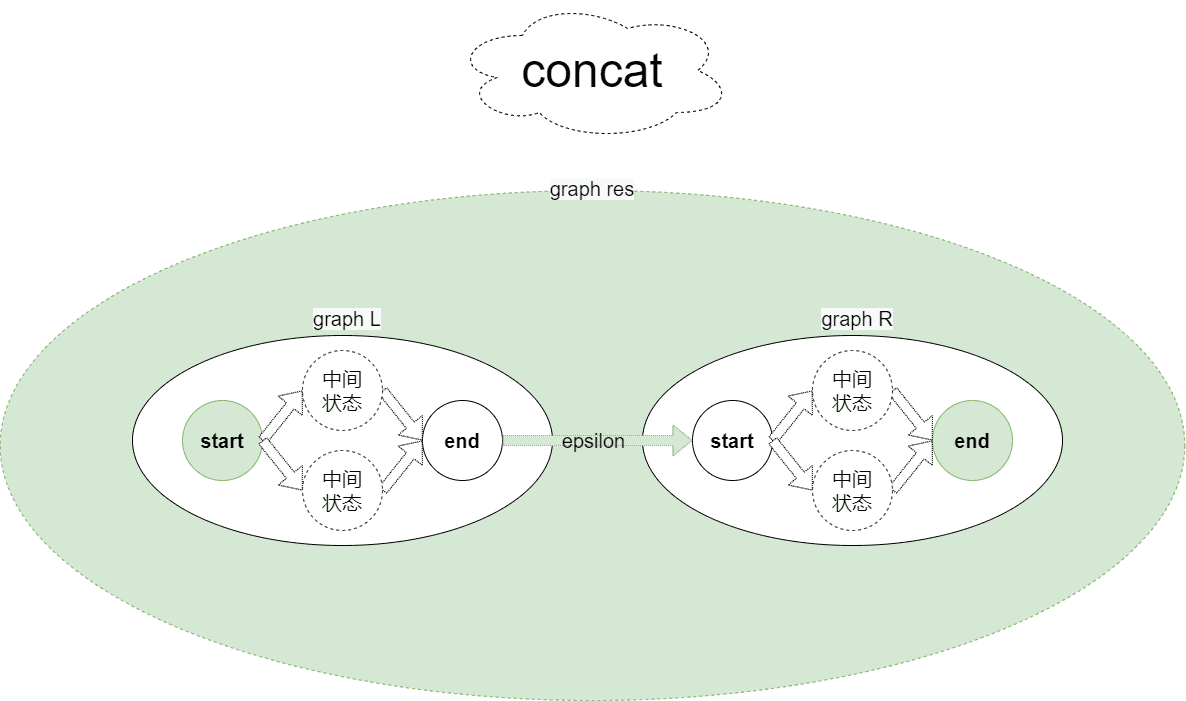
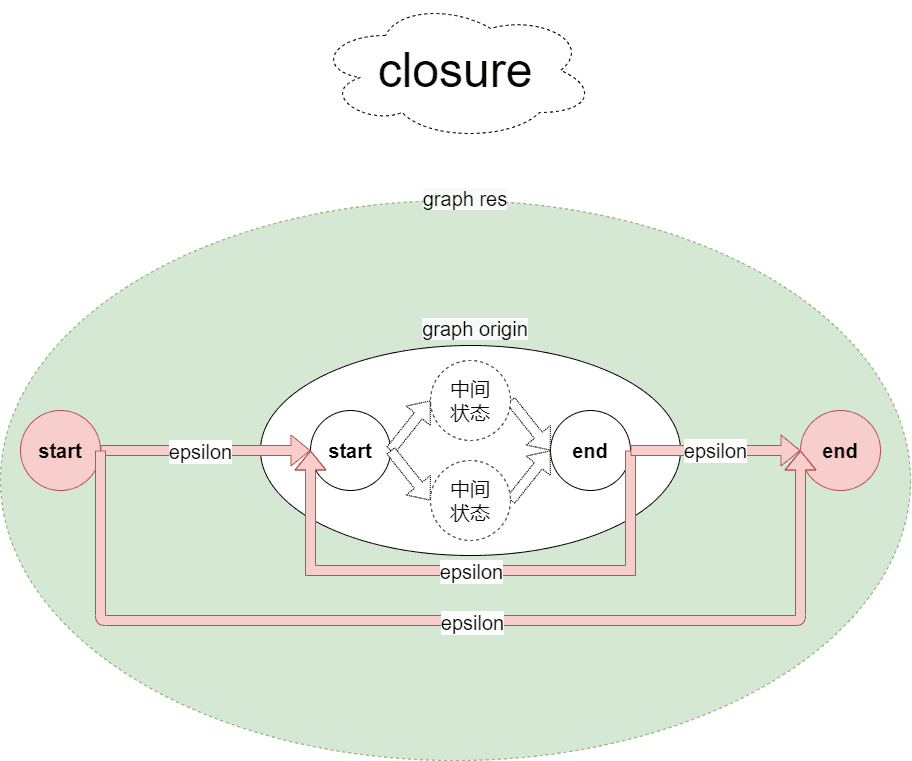
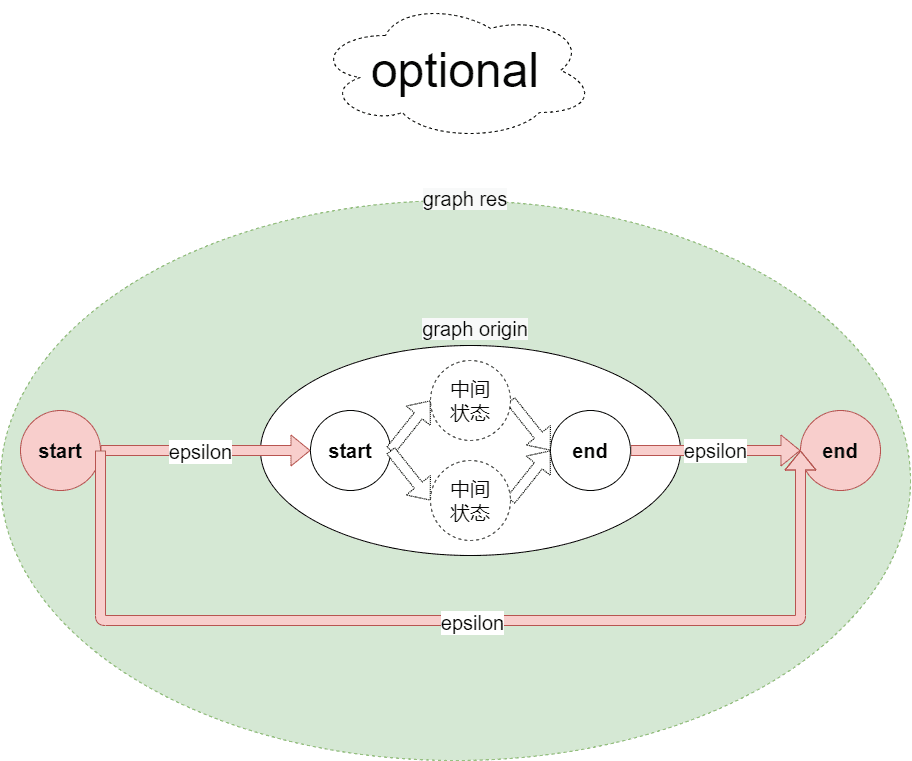
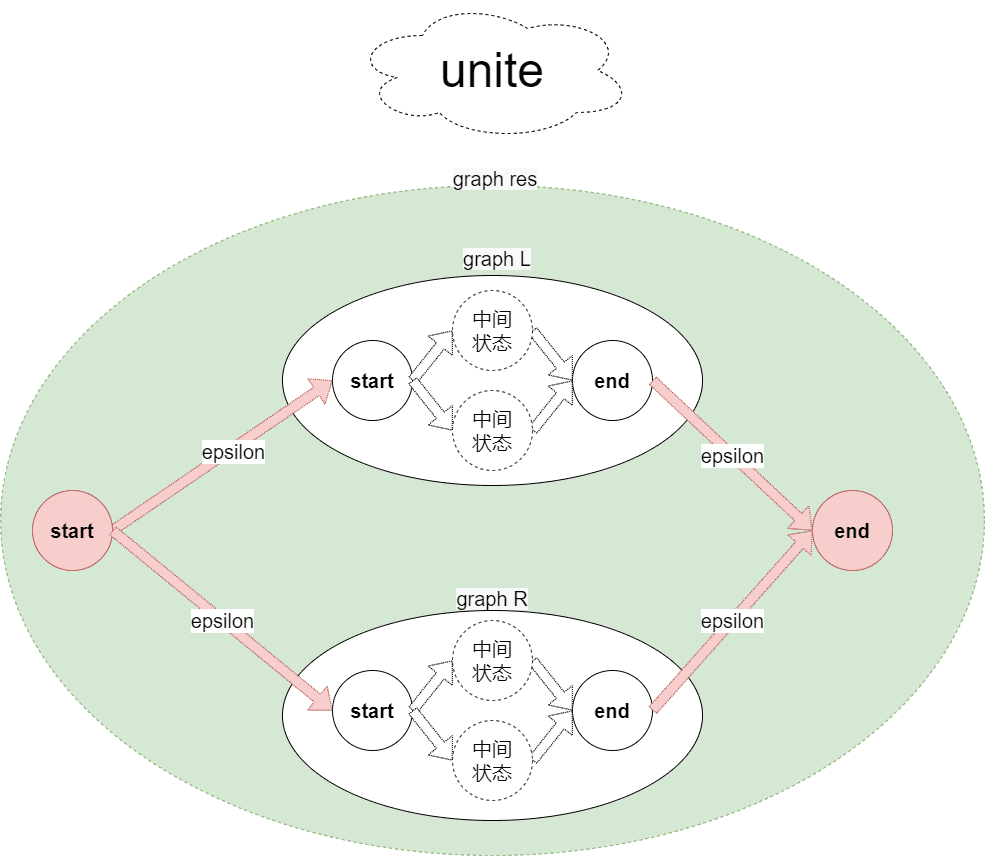
其中的unite、closure、optional、concat函数根据如下图示应该很好理解，每种操作基本都是在给出的原有图上新增起始终止状态和添加epsilon边（NFA允许epsilon转移，那就可以大胆的加边和状态了

查看代码

graph concat(graph l, graph r) {
	graph res(l.start, r.end);
	res.edges.insert(edge(l.end, r.start, epsilon));
	res.edges.insert(l.edges.begin(), l.edges.end());
	res.edges.insert(r.edges.begin(), r.edges.end());
	return res;
}

graph unite(graph l, graph r) {
	graph res = new_graph();

	res.edges.insert(edge(res.start, l.start, epsilon));
	res.edges.insert(edge(res.start, r.start, epsilon));

	res.edges.insert(edge(l.end, res.end, epsilon));
	res.edges.insert(edge(r.end, res.end, epsilon));

	res.edges.insert(l.edges.begin(), l.edges.end());
	res.edges.insert(r.edges.begin(), r.edges.end());

	return res;
}

graph closure(graph origin) {
	graph res = new_graph();

	res.edges.insert(edge(res.start, origin.start, epsilon));
	res.edges.insert(edge(res.start, res.end, epsilon));
	res.edges.insert(edge(origin.end, res.end, epsilon));
	res.edges.insert(edge(origin.end, origin.start, epsilon));

	res.edges.insert(origin.edges.begin(), origin.edges.end());

	return res;
}
graph optional(graph origin) {
	graph res = new_graph();
	res.edges.insert(edge(res.start, origin.start, epsilon));
	res.edges.insert(edge(res.start, res.end, epsilon));
	res.edges.insert(edge(origin.end, res.end, epsilon));
	res.edges.insert(origin.edges.begin(), origin.edges.end());
	return res;
}

graph positive_closure(graph origin) {
	graph res = new_graph();

	res.edges.insert(edge(res.start, origin.start, epsilon));
	res.edges.insert(edge(origin.end, res.end, epsilon));
	res.edges.insert(edge(origin.end, origin.start, epsilon));

	res.edges.insert(origin.edges.begin(), origin.edges.end());

	return res;
}

通过以上的方法，其实我们已经得到了NFA图，但是使用的是边集数组，不好确定某个状态的转移情况，每次都需要遍历一次数组。为了方便表示和后续操作，我们定义二维矩阵来表示NFA, 类似于下表, 可以根据索引很快的知道每个状态的转移情况。

	转移符1	转移符2	转移符ε	...
状态1	状态1经转移符1到达的状态	状态1经转移符2到达的状态	状态1经ε到达的状态
状态2	...	...
...

查看代码

struct NFA {
	vector<char>transfers;
	vector<vector<set<int>>>transfer_table;
	map<char, int>transfer_id;
	int start;
	int end;
	NFA() = default;
	NFA(graph nfa) {
		set<char>transferset;
		set<int>stateset;
		int siz = 0;
		// 1. 去重地记录所有的转移符号和状态
		for (auto& e : nfa.edges) {
			stateset.insert(e.u);
			stateset.insert(e.v);
			transferset.insert(e.w);
		}
		// 2. 记录所有的转移符号的编号, 用以加速寻找其在二维转移矩阵的下标
		transfers = vector<char>(transferset.begin(), transferset.end());
		for (int i = 0; i < transfers.size(); i++) {
			transfer_id[transfers[i]] = i;
		}
		// 3. 获取状态数量,以初始化二维转移矩阵
		siz = stateset.size();
		// 4. 初始化二维转移矩阵, 横是转移字符，竖是每一个状态
		transfer_table.resize(siz);
		for (auto& v : transfer_table) {
			v.resize(transfers.size());
		}
		// 5. 将 边集数组nfa 转换为 二维转移矩阵, 方便以后转换为DFA
		for (auto& e : nfa.edges) {
			int i = e.u;
			int j = transfer_id[e.w];
			transfer_table[i][j].insert(e.v);
		}
		start = nfa.start;
		end = nfa.end;
	}
};

其中transfers维护着NFA的所有转移字符，transfer_id是一个映射关系表，将每个转移字符映射为一个整型下标，用于在矩阵NFA中快速定位某个状态经该转移字符后到达的状态集合，transfer_table是状态转换表，包含着所有的状态转换信息，其中初始状态的数值作为行，转移字符映射的下标作为列，得到该状态经该转移字符后到达的状态集合。同时，也包括两个整型，分别表示整个NFA的起始状态和结束状态，这两个值和Graph中的起始、结束状态的值相同。

NFA→DFA

有了矩阵版的NFA图后，我们可以将NFA转换为DFA，这其中的关键是消除ε转移和多重转移。消除ε转移涉及到了ε闭包的构造。ε-闭包表示从一个状态开始，通过零个或多个ε转移可以到达的所有状态的集合。消除在单个输入字符上的多重转移涉及跟踪可由匹配单个字符而达到的状态的集合。这两个过程都要求考虑状态的集合而不是单个状态，因此这个算法称作子集构造。

查看代码

set<int> epsilon_closure(NFA nfa, int start) {
	if (nfa.transfer_id.count(char(epsilon))) {
		int j = nfa.transfer_id[char(epsilon)];
		return nfa.transfer_table[start][j];
	}
	return {};
}
set<int> epsilon_move(NFA nfa, int start) {
	queue<int>q;
	set<int>vis;
	vis.insert(start);
	q.push(start);
	while (!q.empty()) {
		int cur = q.front();q.pop();
		set<int> to = epsilon_closure(nfa, cur);
		for (int v : to) {
			if (vis.count(v))continue;
			vis.insert(v);
			q.push(v);
		}
	}
	return vis;
}

NFA的一个状态经过ε转移可以到达多个状态, 我们把这些能到达的状态闭包进行编号, 得到NFA的一个状态. 为了方便, 我们给DFA定义新的结构体.

另外, NFA是根据根据graph得到的, 因此开始和结束状态只有一个, 是固定. 但DFA不同, DFA由NFA得到, DFA的每个状态都对应着NFA的某个状态集合, 只要包含了NFA结束状态的状态集合就属于DFA的结束状态, 因此DFA的结束状态也是一个集合.

矩阵版DFA和矩阵NFA类似，不同的是：

1. 每个状态经过特定的转移字符后得到的状态是固定，使用整型来替代，因此transfer_table中的值是整型，其中的整型可能对应的是矩阵NFA中的一个状态集合。
2. DFA的起点状态是NFA起点的空串闭包，是一个固定的状态集合或状态，使用一个整型可以替代表示，DFA 的终态是那些包含原来的终态的状态集，需要使用整型集合表示。

查看代码

struct DFA {
	vector<char>transfers;
	vector<vector<int>>transfer_table;
	map<char, int>transfer_id;
	int start;
	set<int>end;
	DFA() = default;
	DFA(NFA nfa) {
		// 0. DFA中的每个状态是NFA的状态集合,需要将 NFA的状态集合映射 为 新的状态数字
		map<set<int>, int>state_id;
		// 1. 复制nfa的转移字符,然后删除epsilon转移字符,并重新编号
		transfers = nfa.transfers;
		for (auto it = transfers.begin(); it != transfers.end(); it++) {
			if ((*it) == epsilon) {
				transfers.erase(it);
				break;
			}
		}
		for (int i = 0; i < transfers.size(); i++) {
			transfer_id[transfers[i]] = i;
		}

		set<int> eps_start = epsilon_move(nfa, nfa.start);

		int siz = 0;
		state_id[eps_start] = siz++;

		start = state_id[eps_start];
		if (eps_start.count(nfa.end)) {
			end.insert(state_id[eps_start]);
		}

		vector<int>line(transfers.size(), -1); // 整行初始化为-1，表示一个对于所有转移字符不可达的状态
		transfer_table.push_back(line);
		queue<set<int>>q;
		q.push(eps_start);
		while (!q.empty()) {
			set<int> se = q.front();q.pop();
			for (char t : transfers) { // 对于当前一个状态集合se, 每个状态尝试通过转移字符 t 进行转移 
				set<int>to;
				for (int cur : se) { // to记录se中每个状态通过nfa转移表的字符 t 能转移到的状态
					int i = cur;
					int j = nfa.transfer_id[t];
					set<int>tmp = nfa.transfer_table[i][j];
					to.insert(tmp.begin(), tmp.end());
				}
				set<int> eps_to;
				for (auto t : to) { // to转到的状态还不完整, 还需要包含每个状态的epsilon闭包, 即to中每个状态通过epsilon转移
					set<int> eps_t = epsilon_move(nfa, t);
					eps_to.insert(eps_t.begin(), eps_t.end());
				}
				if (eps_to.empty())continue;
				if (!state_id.count(eps_to)) { // 如果是新状态, 给新状态编号, 并且需要将新状态放到队列中, 来计算新状态的转移情况
					state_id[eps_to] = siz++;
					transfer_table.push_back(line);
					q.push(eps_to);
				}

				if (eps_to.count(nfa.end)) {
					end.insert(state_id[eps_to]);
				}
				int i = state_id[se];
				int j = transfer_id[t];
				transfer_table[i][j] = state_id[eps_to];
			}
		}
	}
};

DFA→最小化DFA

自动机理论中有一个很重要的结果，即：对于任何给定的 DFA，都有一个含有最少量状态的等价的DFA，而且这个最小状态的 DFA是唯一的（重命名的状态除外）。我们可以从任何指定的DFA中直接得到这个最小状态的DFA，接下来我们进行DFA的最小化。

定义DFA_minimize函数，接受一个DFA作为输入，并返回一个最小化后的DFA。

函数的主要步骤如下：

1. 初始化分组：根据DFA的结束状态和非结束状态，将状态分为两个初始分组。
2. 进入循环：进入一个循环，直到没有状态集合被拆分为止。
3. 重新编号：为每个状态集合分配一个唯一的编号。
4. 归属关系：为每个状态找到所属的集合编号。
5. 检查转移：对于每个状态集合，检查根据每个转移字符是否会到达不同的状态集合。
6. 拆分状态集合：如果存在转移字符会到达不同的状态集合，则将当前状态集合拆分为多个新的状态集合。
7. 更新循环条件：如果有状态集合被拆分，则继续下一次循环。
8. 构建最小化DFA：根据拆分后的状态集合，构建最小化后的DFA。
9. 返回最小化DFA。

查看代码

set<set<int>> init_group(DFA dfa) {
	set<int>start;
	for (int i = 0; i < dfa.transfer_table.size(); i++) {
		if (!dfa.end.count(i)) {
			start.insert(i);
		}
	}
	set<set<int>>groups;
	if (!start.empty())groups.insert(start);
	groups.insert(dfa.end);
	return groups;
}
struct SetHash {
	size_t operator()(const set<int>& s) const {
		size_t seed = 0;
		for (const int& val : s) {
			seed ^= hash<int>()(val) + 0x9e3779b9 + (seed << 6) + (seed >> 2);
		}
		return seed;
	}
};

struct SetEqual {
	bool operator()(const set<int>& lhs, const set<int>& rhs) const {
		return lhs == rhs;
	}
};
DFA DFA_minimize(DFA dfa) {
	set<set<int>>groups = init_group(dfa); // 初始化分为两组, 一个是包含结束状态, 令一个是不包含
	DFA ans;
	ans.transfers = dfa.transfers;

	bool ok = 0;
	while (!ok) {
		ok = 1;
		// 因为每次循环都会把一个状态集合拆分成多个, 因此需要重新给每个状态集合编号
		unordered_map<set<int>, int, SetHash, SetEqual> set_id;
		//map<set<int>, int> set_id;
		int i = 0;
		for (auto group : groups) {
			set_id[group] = i++;
		}
		// 让每个状态找到所归属的对应集合编号
		unordered_map<int, int>belong_set;
		for(auto group: groups){
			for (auto state : group) {
				belong_set[state] = set_id[group];
			}
		}
		// 判断一个状态集合中的每个状态根据一个转移字符是否会走到不同的状态集合
		for (auto group : groups) {
			for (int j = 0; j < dfa.transfers.size(); j++) {
				char t = dfa.transfers[j];
				map<int, set<int>>mp; // 存储每个状态集合编号下，到达该编号的状态
				for (int i : group) {
					int to = dfa.transfer_table[i][j];
					int belong_to;
					if (to == -1)belong_to = -1; // 无转移也是一种特殊情况
					else belong_to = belong_set[to];
					mp[belong_to].insert(i);
				}
				if (mp.size() > 1) {
					ok = 0;
					groups.erase(group);
					for (auto m : mp) {
						groups.insert(m.second);
					}
				}
			}
			if (!ok)break;
		}
	}

	ans.transfer_table.resize(groups.size());
	for (auto& v : ans.transfer_table) {
		v.resize(dfa.transfers.size());
	}
	map<set<int>, int>mp;
	int siz = 0;
	map<int, int>in_group;
	for (auto g : groups) {
		mp[g] = siz++;
		if (g.count(dfa.start)) {
			ans.start = mp[g];
		}
		for (auto state : g) {
			in_group[state] = mp[g];
			if (dfa.end.count(state)) {
				ans.end.insert(mp[g]);
			}
		}

	}
	for (auto g : groups) {
		int i = *g.begin(); // 对于同一个组中的状态, 其转移情况是一样的, 因此选开头第一个即可
		for (int j = 0; j < dfa.transfers.size(); j++) {
			if (dfa.transfer_table[i][j] == -1) {
				ans.transfer_table[mp[g]][j] = -1;
			} else {
				ans.transfer_table[mp[g]][j] = in_group[dfa.transfer_table[i][j]];
			}
		}
	}
	return ans;
}

DFA→生成C++代码

有了DFA，我们就可以根据状态转移表生成相应的C++代码了。其实就是把状态转移表打印出来，再把转移过程也打印出来。

生成状态转移函数

generate_cpp函数接收一个DFA对象、一个正则表达式和一个数字num作为参数，regex_type作为正则表达式的类型。

DFA对象是第num个正则表达式字符串的DFA。

查看代码

string generate_cpp(DFA dfa, string regex, int num, string regex_type) {
	string cpp;
	cpp += "// " + regex + "\n";
	//cpp += "bool check" + to_string(num) + "() { \n";
	cpp += "bool check_" + regex_type + "() { \n";
	cpp += "    unordered_map<int, unordered_map<char, int>> transfer{\n";
	for (int i = 0; i < dfa.transfer_table.size(); i++) {
		if (i == 0) {
			cpp += "        {\n";
		} else {
			cpp += "        }, {\n";
		}
		cpp += "            " + to_string(i) + ", {\n";
		for (int j = 0; j < dfa.transfers.size(); j++) {
			if (dfa.transfer_table[i][j] == -1)continue;
			cpp += "                {";
			if (dfa.transfers[j] == '\t') {
				cpp += "'\\t'";
			} else if (dfa.transfers[j] == '\n') {
				cpp += "'\\n'";
			} else if (dfa.transfers[j] == '\'') {
				cpp += "'\\''";
			} else {
				cpp += "'" + string(1, dfa.transfers[j]) + "'";
			}
			cpp += ", ";
			cpp += to_string(dfa.transfer_table[i][j]);
			cpp += "},\n";
		}
		cpp += "            }\n";
	}
	cpp += "        }\n";
	cpp += "    };\n\n";
	cpp += "    unordered_set<int> endState = {";
	int siz = dfa.end.size();
	for (int state : dfa.end) {
		if (--siz == 0) cpp += to_string(state) + "};\n";
		else cpp += to_string(state) + ", ";
	}
	//cpp += "    preserve();\n";
	cpp += "    int st = " + to_string(dfa.start) + ";\n\n";

	cpp += "    while(true) {\n";
	cpp += "        char typ = get_char();\n";
	cpp += "        if (transfer[st].find(typ) == transfer[st].end()) { break; }\n";
	cpp += "        else { st = transfer[st][typ]; next_char(); }\n";
	cpp += "    }\n";
	cpp += "    if(endState.count(st)) { return true; }\n";
	cpp += "    else { unget_next_char(); return false; }\n";
	cpp += "}\n";
	return cpp;
}

效果如下

查看代码

// a*(b|c)
bool check1(string s) {
    unordered_map<int, unordered_map<char, int>> transfer{
        {
            0, {
                {'a', 0},
                {'b', 1},
                {'c', 1},
            }
        }, {
            1, {
            }
        }
    };

    int len = s.length();
    unordered_set<int> endState = {1};
    int st = 0;

    for (int i = 0; i < len; i++) {
        char typ = s[i];
        if (transfer[st].find(typ) == transfer[st].end()) {
            return false;
        } else {
            st = transfer[st][typ];
        }
    }
    return endState.count(st);
}

生成词法判断逻辑

generate_tail函数接收一个正则表达式类型的数组和一个数字作为参数。

它首先创建一个空的C++代码字符串，然后添加一个函数定义。

这个函数首先保存当前位置，然后遍历所有的正则表达式类型，对每个类型调用对应的检查函数。

如果检查函数返回true，那么函数返回当前类型，否则恢复保存的位置并继续下一个类型。

如果所有的类型都没有匹配，那么函数返回一个空字符串。

最后，函数添加一段尾部代码，包括主函数的定义和一些错误处理代码。

查看代码

string generate_tail(vector<string>regex_types, int num) {
	string cpp = "\n\n";
	cpp += "string get_token(){\n";
	cpp += "    bool matched = false;\n\n";
	cpp += "    preserve();\n";
	for (int i = 1; i <= num; i++) {
		cpp += "    matched = check" + to_string(i) + "();\n";
		cpp += "    if(matched){ return \"" + regex_types[i-1] + "\";}\n";
		cpp += "    else { recover(); }\n";
	}
	cpp += "    return \"\";\n";
	cpp += "}\n";
	cpp += tail;
	return cpp;
}

定义固定的头部

head字符串包含一些基本的C++库的引用，如<string>、<iostream>、<fstream>、<unordered_set>和<unordered_map>。

然后，定义一些全局变量和函数，这些函数用于处理输入字符串的字符。

查看代码

string head = R"(#include<string>
#include<iostream>
#include <fstream>
#include<unordered_set>
#include<unordered_map>
using namespace std;

string content;
int i, origin;
bool got_char = false;
char get_char() { return i == content.size() ? '\0' : content[i]; }
void next_char() { got_char = true; i++; }
void unget_next_char() { if(got_char) got_char = false, i--; }
void preserve() { origin = i; }
void recover() { i = origin; }

)";

定义固定的尾部

tail字符串包含一个main函数的定义，用于词法分析。这个函数接受一个文件路径作为参数。

这个函数首先检查命令行参数的数量，如果参数数量不正确，就打印一个错误消息并返回1。

然后，它打开输入文件并检查是否成功。如果文件打开失败，就打印一个错误消息并返回1。

接着，它将输入文件的内容读入到全局变量content中。

然后，它创建一个输出文件到当前项目的路径下，名称为"sample.lex"。如果文件创建失败，就打印一个错误消息并返回1。

接下来，它进入一个循环，不断调用get_token函数并将结果写入到输出文件中，直到get_token函数返回空字符串。

最后，它关闭输出文件并返回0。

sample.lex文件中的单词编码格式如下：

[]中是输入中的一个字符串，然后是一个空格，接着是这个字符串的单词编码类型，

如[=] equal，表示=是equal类型。

查看代码

string tail = R"(
int main(int argc, char* argv[]) {
    if (argc != 2) {
        cerr << "Usage: " << argv[0] << " <input_file_path>" << endl;
        return 1;
    }
    string inputFilePath = argv[1];
    ifstream inputFile(inputFilePath);
    if (!inputFile.is_open()) {
        cerr << "Error: Unable to open input file" << endl;
        return 1;
    }
    content.assign((std::istreambuf_iterator<char>(inputFile)), std::istreambuf_iterator<char>());
    ofstream outputFile("sample.lex");
    if (outputFile.is_open()) {
        while (true) {
            string cur = get_token();
            if (cur == "") {
                if (i != content.size()) {
                    outputFile << "Error: position in " << i << endl;
                }
                break;
            } else {
                if (cur == "space")continue;
                outputFile << "[" << content.substr(origin, i - origin) << "] ";
                outputFile << cur << "\n";
            }
        }
        outputFile.close();
        cout << "File content saved to sample.lex" << endl;
    } else {
        cerr << "Error: Unable to create output file" << endl;
        return 1;
    }
    return 0;
})";

编译词法分析代码

我们打开一个名为 "output.cpp" 的输出文件流对象 outputFile，以便将生成的C++代码写入到该文件中。

然后使用系统调用 system("cmd /k cl /EHsc output.cpp") 来调用命令行编译器（这里是 Visual Studio 中的 C/C++ 编译器 cl.exe）编译生成的 output.cpp 文件。

编译成功后会在当前目录下生成output.exe和outout.obj。

其中output.exe为可执行文件，在命令行中指定一个文件路径作为参数，就可以对该文件进行词法分析了，输出的结果为一个sample.lex文件。

以上就是本次分享的主要内容，希望能够帮助大家更好地理解和应用编译原理的概念。如果大家有任何问题或疑惑，都可以随时向我提问。我会尽力帮助大家解决。

如果需要完整的有图形界面展示的代码，请在下方留言哦。